F# i Regresja Liniowa

Ostatnio implementowaliśmy w F# prosty przykład, ilustrujący wykorzystanie Gradientu Prostego do znalezienia minimum wybranej funkcji.
Dziś zdobyte doświadczenie wykorzystamy do czegoś bardziej praktycznego – przewidywania wysokości wynagrodzenia w zależności od doświadczenia.

Dane

Wykorzystamy publicznie dostępny, prosty zbiór zawierający fikcyjne dane, który dzięki swojej prostocie ułatwi zrozumienie tematu:

https://www.kaggle.com/datasets/abhishek14398/salary-dataset-simple-linear-regression

Chociaż wykorzystamy fikcyjne dane, sposób budowy modelu umożliwiającego predykcję będzie jak najbardziej rzeczywisty.

Type Providers

Dane dostępne są w postaci pliku csv, co będzie pretekstem do skorzystania z wygodnego narzędzia języka F# – dostawcy typów (ang. „type provider”). W tym konkretnym przypadku będzie to CsvProvider, dostępny w bibliotece FSharp.Data.

CsvProvider pozwala na generowanie typów F# na podstawie struktury danych w plikach csv. Dzięki temu nie będziemy musieli ręcznie definiować typów danych w kodzie F#, a uzyskamy korzyści płynące z silnego, statycznego typowania w F#.

W naszym przypadku plik z danymi zawiera listę obserwacji opisanych następującymi cechami:

• Index – liczba porządkowa, nieistotna z naszego punku widzenia
• YearsExperience – doświadczenie liczone w latach
• Salary – wynagrodzenie

Do zdefiniowania typu dla badanego zbioru danych oraz pojedynczej obserwacji wystarczy następująca linia:

type Data = CsvProvider<"salary_dataset.csv", ResolutionFolder=__SOURCE_DIRECTORY__>
type Observation = Data.Row

Teraz pozostaje nam załadować dane z pliku i przekształcić w kolekcję obserwacji:

let data = Data.Load(__SOURCE_DIRECTORY__ + "/salary_dataset.csv")
let observations = data.Rows

Korzystając z silnego typowania możemy w prosty sposób odnosić się do poszczególnych cech obserwacji:

observations
|> Seq.iter (fun o -> printfn $"%.1f{o.YearsExperience} -> %.2f{o.Salary}")

Każda z obserwacji ma zdefiniowane cechy o nazwach zgodnych z nagłówkiem pliku csv i co nie mniej ważne, z przypisanym typem (w tym wypadku decimal). Dokładnie tak jak gdybyśmy sami wcześniej zdefiniowali ten typ, sparsowali plik i zbudowali z niego kolekcję rekordów.

Obserwacje

Spróbujmy zwizualizować badany zbiór obserwacji.

Zaczniemy od pomocniczej funkcji odpowiedzialnej za formatowanie i wyświetlanie wykresów:

let showChart (charts: GenericChart seq) =
    charts
    |> Chart.combine
    |> Chart.withSize (1000., 600.)
    |> Chart.withTitle "Salary vs Experience"
    |> Chart.withXAxisStyle ("Years of Experience")
    |> Chart.withYAxisStyle ("Salary")
    |> Chart.show

Teraz zdefiniujmy wykres prezentujący badane obserwacje i spróbujmy go wyświetlić:

let observationsChart =
    observations
    |> Seq.map (fun o -> o.YearsExperience, o.Salary)
    |> Chart.Point
    |> Chart.withTraceInfo ("Observations")

showChart [ observationsChart ]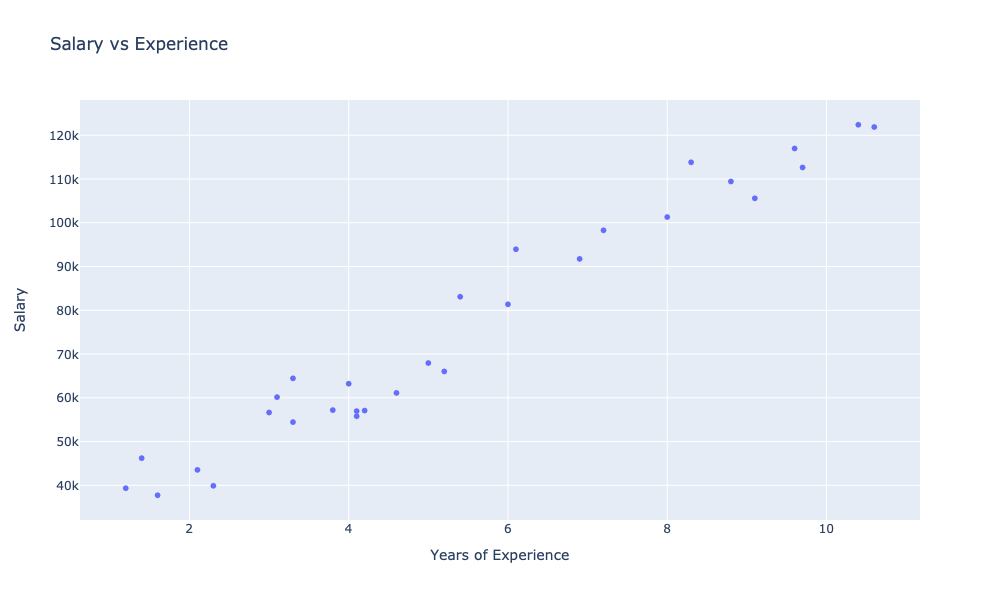

Na wykresie widzimy zależność poziomu wynagrodzenia od doświadczenia. Gołym okiem możemy zaobserwować widoczny silny związek pomiędzy wynagrodzeniem a doświadczeniem.
Taką zależność możemy wyrazić liczbowo, w postaci tzw. współczynnika korelacji.

Możemy zaimplementować własną funkcję wykorzystując wzór:

r = Σ((xi – x̄)(yi – ȳ)) / √(Σ(xi – x̄)² * Σ(yi – ȳ)²)

Gdzie:

• xi i yi to poszczególne wartości zmiennych X i Y,
• x̄ i ȳ to średnie wartości zmiennych X i Y,
• Σ oznacza sumowanie po wszystkich obserwacjach (i = 1, 2, …, n),
• n to liczba obserwacji.

My dla uproszczenia skorzystamy z kolejnej świetnej biblioteki: Fsharp.Stats

observations
|> pearsonBy (fun o -> o.YearsExperience, o.Salary)
|> printfn "Pearson correlation: %.2f"

Tak czy inaczej uzyskamy wynik 0.98 co wskazuje na bardzo silną korelację dodatnią (obie cechy rosną proporcjonalnie). Wynik bliski zeru świadczyłby o braku korelacji pomiędzy cechami natomiast wynik bliski -1 oznaczałby silną korelację ujemną (wzrost jednej cechy powoduje proporcjonalny spadek drugiej).

Domena

Naszym celem będzie implementacja modelu który będzie przewidywał możliwie skutecznie wynagrodzenie dla podanego doświadczenia.

Zacznijmy od zdefiniowania domeny problemu:

type Experience = decimal

type Salary = float

type Model = Experience -> Salary

Puryści projektowania sterowanego domeną (tzw. DDD) byliby zachwyceni 😉

Model bazowy

Teraz aby móc się do czegoś odnosić zdefiniujmy możliwie prosty i naiwny model. Przyjmijmy założenie iż model ten bez względu na doświadczenie zwracać będzie średnią zarobków:

let averageModel (experience: Experience) =
    observations |> Seq.averageBy (fun o -> o.Salary) |> float

Aby móc porównywać przyszłe modele do tego bazowego, potrzebujemy jakiejś metody oceny skuteczności modelu. Musimy określić metrykę jakości.

Metryka – suma kwadratów reszt

Skorzystamy z tzw. sumy kwadratów reszt (SSE, ang. Sum of Squared Errors) czyli różnicy pomiędzy przewidywaną a rzeczywistą wartością.
Zacznijmy od wzoru:

SSE = Σ(yi – ŷi)²

Gdzie:

• yi to rzeczywista wartość i-tej obserwacji,
• ŷi to przewidywana wartość i-tej obserwacji,
• Σ oznacza sumowanie po wszystkich obserwacjach (i = 1, 2, …, n),
• n to liczba obserwacji.

let sse (obs: Observation seq) (model: Model) =
    obs
    |> Seq.sumBy (fun o -> (model o.YearsExperience - float o.Salary) ** 2.0)

Teraz możemy ocenić nasz bazowy model:

let avgModelScore = sse observations averageModel

następnie zdefiniować dla niego wykres i zwizualizować:

let scoreFormat = "N2"

let avgModelChart =
    observations
    |> Seq.map (fun o -> o.YearsExperience, averageModel o.YearsExperience)
    |> Chart.Line
    |> Chart.withTraceInfo $"%s{avgModelScore.ToString(scoreFormat)} - Base model"

showChart [ observationsChart; avgModelChart ]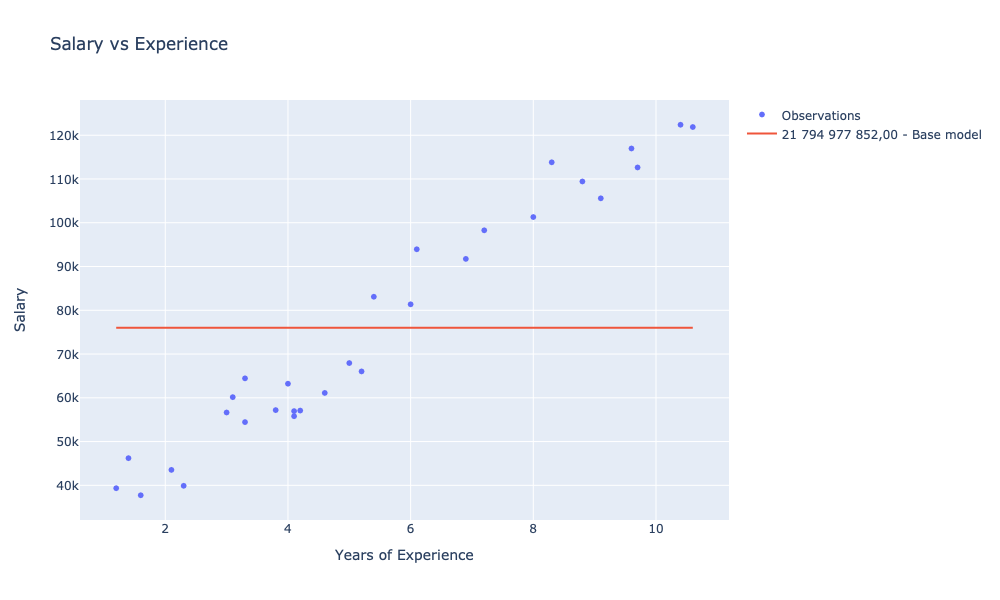

Regresja Liniowa

Regresja liniowa to technika statystyczna używana do analizy relacji pomiędzy dwiema zmiennymi – zmienną niezależną (w naszym przypadku doświadczenie) i zmienną zależną (w naszym przypadku wynagrodzenie). Celem regresji liniowej jest znalezienie najlepszego dopasowania linii prostej do danych, które pozwoli na przewidywanie wartości zmiennej zależnej na podstawie wartości zmiennej niezależnej.

Wzór na prostą w przestrzeni dwuwymiarowej definiuje równanie y = theta1 * x + theta0 gdzie:

• y to zmienna zależna
• x to zmienna niezależna
• theta1 to współczynnik kierunkowy prostej
• theta0 to wyraz wolny

Naszym zadaniem będzie znalezienie takich theta0 i theta1 dla których SSE będzie najmniejszy. Skorzystamy z Gradientu, bardziej szczegółowo opisanego tutaj.
Będziemy aktualizować współczynniki obliczając wartość pochodnej cząstkowej dla zmiennej niezależnej osobno dla każdego współczynnika. Pochodne obliczymy korzystając m. in z reguł: łańcuchowej i potęg.

Funkcja aktualizująca wartości współczynników może wyglądać tak:

let updateThetas (alpha: float) (theta0, theta1) (obs: Observation) =
    let x = float obs.YearsExperience
    let y = float obs.Salary
    let theta0' = theta0 - 2. * alpha * (theta0 + theta1 * x - y)
    let theta1' = theta1 - 2. * alpha * x * (theta0 + theta1 * x - y)
    (theta0', theta1')

Dla podanej obserwacji „przesuwamy” wartości poszczególnych współczynników theta w kierunku ujemnym gradientu – odejmujemy kolejno wartość pochodnej pomnożonej o stałą uczenia alfa.

Gradient stochastyczny

Zaczniemy od prostszego algorytmu – gradientu stochastycznego który pozwala na szybszą i bardziej efektywną optymalizację funkcji błędu. W przypadku gradientu stochastycznego, obliczenie gradientu funkcji błędu odbywa się tylko dla pojedynczego przykładu treningowego w każdej iteracji algorytmu. W ten sposób, algorytm ten jest bardziej skuteczny dla dużych zbiorów danych, ponieważ wymaga mniejszej ilości obliczeń i nie jest uzależniony od całego zestawu danych.

Zaletą gradientu stochastycznego jest szybkość działania i zdolność do osiągania dobrych wyników dla dużej liczby danych treningowych. Wadą natomiast jest większa niestabilność algorytmu i większe prawdopodobieństwo, że algorytm osiągnie lokalne minimum zamiast globalnego.

Implementacja w F# sprowadza się do:

let stochasticGradient alfa (theta0, theta1) (data: Observation seq) =
    data |> Seq.fold (updateThetas alfa) (theta0, theta1)

Jesteśmy niemal gotowi do wytrenowania pierwszego modelu.

Zacznijmy od ogólnej funkcji realizującej Model:

let model (theta0, theta1) (experience: Experience) = float experience * theta1 + theta0

Teraz możemy już wykorzystać wszystkie narzędzia aby wytrenować pierwszy model:

let stochasticModel = stochasticGradient 0.0123 (0., 0.) observations |> model

Wartość stałej uczenia alfa została dobrane empirycznie i powinna być dostosowywana każdorazowo do konkretnego problemu i zestawu danych.
Zachęcam do eksperymentowania.

Możemy ocenić nasz nowy model:

let stochasticModelScore = sse observations stochasticModel

a następnie go zwizualizować:

let stochasticModelChart =
    observations
    |> Seq.map (fun o -> o.YearsExperience, stochasticModel o.YearsExperience)
    |> Chart.Line
    |> Chart.withTraceInfo ($"%s{stochasticModelScore.ToString(scoreFormat)} - Stochastic Model")

showChart [ observationsChart; avgModelChart; stochasticModelChart ]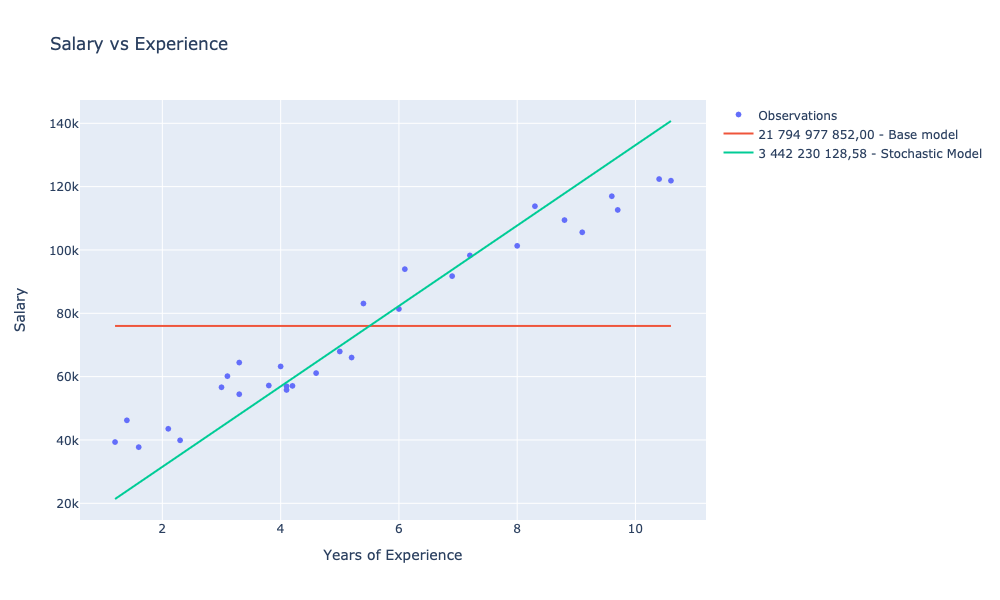

Gradient zbiorczy

Tym razem, dla odmiany, będziemy aktualizować wartości parametrów theta wykorzystując cały zbiór obserwacji w każdej iteracji – stąd nazwa Gradient wsadowy lub zbiorczy (ang. Batch gradient).

Zdefiniujmy funkcję która będzie implementować pojedynczą iterację w oparciu o cały zbiór obserwacji:

let batchUpdateThetas rate (theta0, theta1) (data: Observation seq) =
    let thetas = data |> Seq.map (updateThetas rate (theta0, theta1))

    let theta0' = thetas |> Seq.averageBy fst
    let theta1' = thetas |> Seq.averageBy snd
    (theta0', theta1')

oraz funkcję która będzie szukać optymalnych parametrów theta zadaną ilość razy:

let batchEstimation rate iters (data: Observation seq) =
    let rec search (theta0, theta1) i =
        if i = 0 then
            (theta0, theta1)
        else
            search (batchUpdateThetas rate (theta0, theta1) data) (i - 1)

    search (0., 0.) iters

Teraz możemy wytrenować kolejny model. Przyjmiemy identyczną stałą uczenia i 1 000 powtórzeń:

let batchModel = batchEstimation 0.0123 1_000 observations |> model

Pozostaje nam ocena modelu i jego wizualizacja:

let batchModelCost = sse observations batchModel

let batchModelChart =
    observations
    |> Seq.map (fun o -> o.YearsExperience, batchModel o.YearsExperience)
    |> Chart.Line
    |> Chart.withTraceInfo $"%s{batchModelCost.ToString(scoreFormat)} - Batch Model"

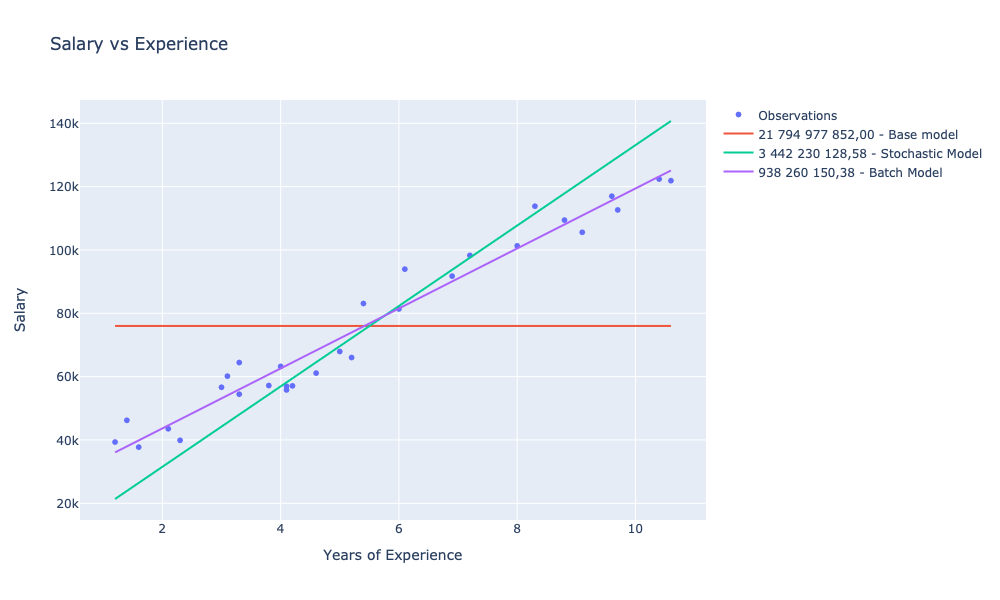
showChart [
    observationsChart
    avgModelChart
    stochasticModelChart
    batchModelChart
]

Podsumowanie

W stosunku do naszego bazowego modelu, dla którego SSE wyniosło 21 794 977 852,00 udało nam się wytrenować dwa modele dla których SSE było mniejsze kolejno o:

• 84% (3 442 230 128,58) dla gradientu stochastycznego
• 95% ( 938 260 150,38) dla gradientu wsadowego

Zachęcam do eksperymentów z ilością iteracji oraz stałą uczenia.

Warto też zaznaczyć iż w produkcyjnym podejściu nie powinniśmy trenować i oceniać modelu przy pomocy tych samych danych.
Powinniśmy zadbać o to aby mieć do czynienia z wydzielonym zbiorem treningowym oraz testowym.

Przydatne linki

• F# i gradient prosty: jak w kilka minut znaleźć minimum funkcji?
• FSharp.Data
• FSharp.Stats
• Suma kwadratów reszt

Kompletny kod

[gist id=”360259b4ae4307372f1516827083649b”]