F# i gradient prosty: jak w kilka minut znaleźć minimum funkcji?

Można go wykorzystać do znajdowania ekstremów funkcji – przykładowo jej minimum. W tym celu, należy obliczyć gradient funkcji w punkcie, który nas interesuje, a następnie poruszać się w kierunku przeciwnym do gradientu, aż dojedziemy do punktu, w którym gradient wynosi zero – oznacza to, że osiągnęliśmy minimum.

Aby lepiej zrozumieć działanie gradientu, przedstawię prosty przykład obliczenia minimum funkcji.

F#

Skorzystam z narzędzia, które wydaje się świetnie sprawdzać w środowisku metod numerycznych, funkcji i algorytmów optymalizacji – języka F#.

F# to tzw. „functional first programming language”, który co prawda umożliwia tworzenie kodu zgodnego np. z paradygmatem obiektowym ale swoją prawdziwą „moc” ujawnia gdy trzymamy się podejścia funkcyjnego. Jest językiem silnie typowanym, zapewnia interoperacyjność – możemy korzystać z bogatego ekosystemu bibliotek i narzędzi .NET oraz dojrzałego modelu asynchroniczności.

Przykładowa implementacja

Zacznijmy od zdefiniowania zależności.

#r "nuget: Plotly.NET"  
  
open System  
open Plotly.NET

Następnie zdefiniujmy na potrzeby przykładu funkcję, której minimum będziemy szukać

// f(x) = (x - 3)^2 + 5  
let f x = (x - 3.) ** 2. + 5.

Dla przejrzystości możemy ją sobie zwizualizować (z wykorzystaniem biblioteki Plotly.NET):

[ -12 .. 18 ]  
|> List.map (fun x -> (float x, f (float x)))  
|> Chart.Line  
|> Chart.withTitle "f(x) = (x - 3)^2 + 5"  
|> Chart.show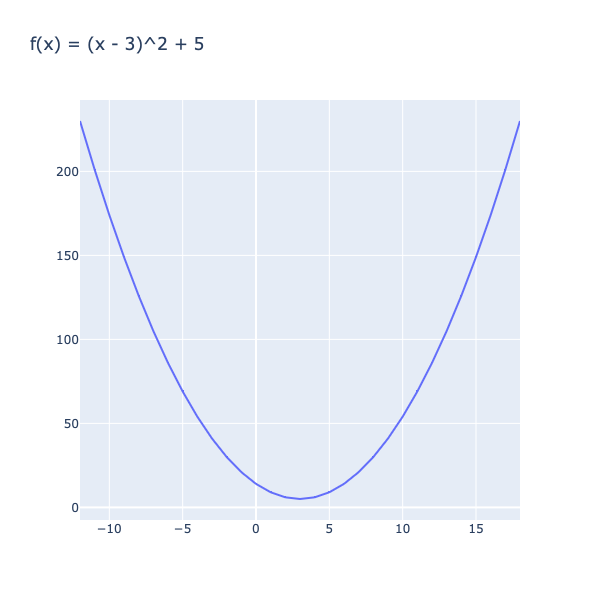

Wykorzystamy metodę gradientu aby znaleźć x, dla którego nasza funkcja osiąga swoje minimum.

Pierwszym krokiem będzie określenie pochodnej badanej funkcji:

// f'(x) = 2(x - 3)  
let dx_f x = 2. * (x - 3.)

Algorytm, który pozwoli nam takie minimum znaleźć będzie działał wg. prostej zasady:

1. Zaczniemy od wygenerowania pseudolosowej wartości X
2. Ustalimy tzw. stałą uczenia (alfa)
3. Ustalimy zakładaną liczbę iteracji
4. Obliczymy gradient funkcji dla X – czyli wartość jej pochodnej w tym punkcie
5. Przesuniemy nasz X w kierunku ujemnym gradientu – czyli w kierunki spadku funkcji. Sprowadzi się to do odjęcia od X gradientu pomnożonego przez stałą uczenia
6. Kroki 4 i 5 będziemy powtarzać aż do osiągnięcia założonej liczby iteracji

// 1
// initial guess  
let rnd = Random(532123)  
let x = rnd.NextDouble() * 100.

// 2
// learning rate  
let alfa = 0.001  

// 3  
// iterations  
let i = 10_000  

// 4 - 5
// performs a single step of gradient descent by calculating the current value of x  
let gradientStep alfa x =  
	let dx = dx_f x
	// show the current values of x and the gradient dx_f(x)  
	printfn $"x = %.20f{x}, dx = %.20f{dx}"  
	x - alfa * dx  

// 6  
// uses gradientStep to find the minimum of f(x) = (x - 3)^2 + 5  
let findMinimum (alfa: float) (i: int) (x: float) =  
	let rec search x i =  
		if i = 0 then x else search (gradientStep alfa x) (i - 1)  
	search x i

Pozostaje nam już tylko wywołać zaimplementowaną funkcję ze zdefiniowanymi wcześniej parametrami:

findMinimum alfa i x |> printfn "'f(x) = (x-3)^2 + 5' reaches a minimum at 'x' = %.20f"

aby otrzymać wynik zbliżony do:

'f(x) = (x-3)^2 + 5' reaches a minimum at 'x'  = 3.00000004479085946585

Oczywiście, w przypadku tak prostych funkcji łatwiej jest znaleźć minimum przy pomocy miejsca zerowego pochodnej, jednak w bardziej złożonych problemach, takich jak chociażby regresja liniowa gdzie minimalizować będziemy funkcję błędu, gradient sprawdzi się świetnie.

Przykład takiej regresji wkrótce…

Przydatne linki

1. F# i Regresja Liniowa
2. https://fsharp.org
3. https://fsharpforfunandprofit.com
4. https://learn.microsoft.com/pl-pl/dotnet/
5. https://ocw.mit.edu/courses/18-01sc-single-variable-calculus-fall-2010/

Kompletny kod

[gist id=”d1eaf03f5fa6585dfc2ef6d7e4fedd61″]